線形回帰と誤差の話。 - いものやま。

機械学習の基本中の基本ともいえる線形回帰。そんな線形回帰も「当たり前」に踏み込んで考えてみるといろいろ面白かったりするので、今日はその話をしてみたい。

これは数理最適化 Advent Calendar 2022の11日目の記事です。

線形回帰のおさらい

たとえば気温とビールの売れた量を見てみたら、次のようになっていたとする：

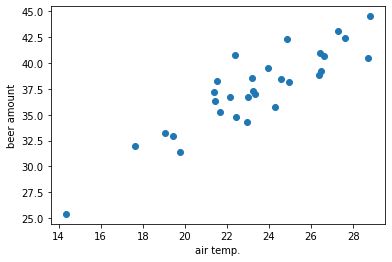
気温が上がればビールも売れていて、なんとなく直線で近似できそうな感じがする。そこで気温を $x$ , ビールの売れた量を $y$ で表すことにして、いい感じの $a, b$ を使って $y = a x + b$ と表現しようというのが線形回帰。

ここで教師データとして実際に現れた気温と売り上げ量のペア $\{(x_i, y_i)\}$ が与えられたとして、適切な $a, b$ を推定したいとする。

さて、気温 $x_i$ に対する予測値は $a x_i + b$ なのに対し、実際には $y_i$ だったので、誤差は $|y_i - (a x_i + b)|$ となる。これは $a, b$ に関する関数となっていて、 $a, b$ の値を変えることで誤差は大きくなったり小さくなったりする。それなら誤差ができるだけ小さくなるような $a, b$ が適切な $a, b$ だといえるだろう。

そこで誤差を最小にするような $a, b$ を探したいんだけど、絶対値をとった誤差だと微分ができなくて都合が悪い。なので絶対値をとる代わりに二乗した誤差 $\left(y_i - (a x_i + b)\right)^2$ の和を考え、これを最小化する。すなわち、次のような $a, b$ を求める：

$\displaystyle \min_{a, b} \sum_{i} \left(y_i - (a x_i + b)\right)^2$

これは解析的に解けて、最適な $a, b$ が簡単に分かる。

Pythonでもscikit-learnのLinearRegressionを使えばサクッと $a, b$ が分かる。

コード例は以下：

import numpy as np
from sklearn.linear_model import LinearRegression

# 気温とビールのデータ
np.random.seed(0)  # データの固定
air_temp = np.random.normal(22, 3, size=30)
true_coef, true_intercept = 1.2, 10
beer = true_coef * air_temp + true_intercept + np.random.normal(0, 2, size=len(air_temp))

# 線形回帰
regressor = LinearRegression()
regressor.fit(air_temp.reshape((-1, 1)), beer)

# 求まった傾きと切片
print(regressor.coef_)  # => [1.08203242]
print(regressor.intercept_)  # => 12.172971204120916

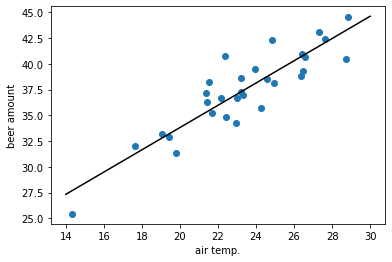
推定した直線を描画するとこんな感じ：

絶対誤差のまま解く線形回帰

ところで、線形回帰の説明でよく出てくる次の言葉。

絶対値をとった誤差だと微分ができなくて都合が悪い

これは本当だろうか？

ほとんどの人は気にしたことないと思うし、別に二乗誤差で解けてるんだから気にする必要もないかと思う。でもそこを突っ込んで考えてみると面白いことが見えてきたりする。

二乗誤差にしないで絶対値をとった誤差のまま最適な $a, b$ を求めるというのは、次の問題を解くということだ：

$\displaystyle \min_{a, b} \sum_{i} \left|y_i - (a x_i + b)\right|$

ここで線形計画問題のテクニックとして覚えておきたいのが、絶対値の値を最小化したい場合には非負の補助変数を導入して補助変数で上下から挟んでやればいいという方法。

$\min_a |a| \quad\Leftrightarrow\quad \mathrm{min.}\; m,\; \mathrm{sub.\ to} -m \le a \le m, m \ge 0$

そこでこの問題も非負の補助変数 $m_i \ge 0$ を導入すると、次のように書ける：

$\displaystyle \left| \begin{array}{rl} \mathrm{min.} & \sum_i m_i \\ \mathrm{sub.\ to} & - m_i \le y_i - (a x_i + b) \le m_i \quad (\forall i) \\ & m_i \ge 0 \quad (\forall i) \\ \end{array} \right.$

つまり、線形計画問題を使えば二乗誤差にしなくても絶対誤差のままで解けたりする。

コード例は以下：

import pulp

# air_temp, beerは上で使ったものを使用

# 問題
problem = pulp.LpProblem(sense=pulp.LpMinimize)

# 変数
coef = pulp.LpVariable("coef")
intercept = pulp.LpVariable("intercept")
error = pulp.LpVariable.dicts("error", range(len(air_temp)), lowBound=0)

# 目的変数
problem += pulp.lpSum(error)

# 制約
for i in range(len(air_temp)):
    predict = coef * air_temp[i] + intercept
    problem += - error[i] <= (predict - beer[i])
    problem += (predict - beer[i]) <= error[i]

# 求解
solver = pulp.PULP_CBC_CMD(msg=False)
status = problem.solve(solver)

# 出力
print(pulp.LpStatus[status])  # => Optimal
print(coef.value())  # => 1.1527883
print(intercept.value())  # => 10.492206

こちらもサクッと解ける。

推定した直線を描画するとこんな感じ：

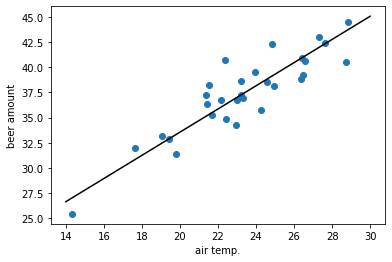
こちらでもいい感じに直線が引けてるのが分かるかと思う。

ところで、二乗誤差でなく絶対誤差でも線形回帰が解けることは分かったけど、じゃあわざわざ絶対誤差で解く必要があるんだろうか。実はこれは「ある」で、絶対誤差で解くことによる応用がいろいろあったりする。

外れ値に強い

まずシンプルに分かりやすいのが、外れ値に強いということ。

機械学習の評価指標でRMSE（Root Mean Squared Error）とMAE（Mean Absolute Error）があって、前者は二乗誤差（をベースにした誤差）、後者は絶対誤差に相当するものとなっている。ここで外れ値を含むようなデータでRMSEをとると値が大きくなりやすく、そういう場合はMAEで評価した方がいいとよく言われている。

これはなぜかというと、二乗誤差は誤差を二乗するので正解から離れていればいるほど誤差の値が急激に大きくなり、外れ値の誤差は普通よりも重く評価されてしまうから。

同じことが線形回帰でも起こって、二乗誤差を最小化する通常の線形回帰だとできるだけ外れ値をなくそうとするので外れ値に敏感に反応してしまう。一方、絶対誤差を最小化する線形回帰であれば外れ値であってもそれを特別視することはないので影響を減らすことができる。

実際、次のように外れ値を追加して試してみる：

# 外れ値を追加；めっちゃ暑かったのでビールがめっちゃ売れた
air_temp_outlier = np.append(air_temp, 32)
beer_outlier = np.append(beer, 32 * true_coef + true_intercept + 10)

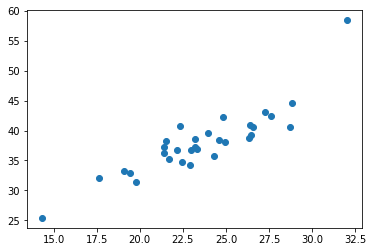
これを二乗誤差を使った普通の線形回帰で解くと、傾きは1.08から1.33へ、切片は12.2から6.63へ変化する。

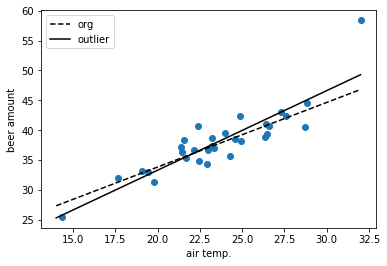
ところが、絶対誤差を使った線形回帰だと、傾きは1.15が1.16へ、切片は10.5が10.3へ変化する程度に留まる。

このように外れ値に強いのがまず大きなメリット。

知識や他の制約を入れられる

線形回帰を線形計画問題に帰着してるので、線形計画問題で表現できる知識を入れたり、あるいは問題に合わせて制約を追加したりということが可能になる。

たとえばこの問題で「傾きは感覚として1.2〜1.5だと思うんだよね」というのであれば、それを素直に制約として追加できる：

# 問題
problem = pulp.LpProblem(sense=pulp.LpMinimize)

# 変数
coef = pulp.LpVariable("coef", lowBound=1.2, upBound=1.5)  # 知識を表現
intercept = pulp.LpVariable("intercept")
error = pulp.LpVariable.dicts("error", range(len(air_temp)), lowBound=0)

# 目的変数
problem += pulp.lpSum(error)

# 制約
for i in range(len(air_temp)):
    predict = coef * air_temp[i] + intercept
    problem += - error[i] <= (predict - beer[i])
    problem += (predict - beer[i]) <= error[i]

# 求解
solver = pulp.PULP_CBC_CMD(msg=False)
status = problem.solve(solver)

# 出力
print(pulp.LpStatus[status])  # => Optimal
print(coef.value())  # => 1.2
print(intercept.value())  # => 9.3041757

見てのとおり、制約が守られた解が得られている。

通常の線形回帰で重みに関する制約を入れようとするとL1の正則項を追加するLasso回帰やL2の正則項を追加するRidge回帰になるけど、これらは重みが0付近に存在することが前提となるし（スケーリングなどして対処することになる）、ペナルティの重みをどうすべきかもなかなか難しい。

あるいは制約付き最小二乗法を使ったりすることになるんだけど、これもなかなか大変。

一方で線形の制約で縛るなら（線形計画問題に慣れてれば）かなり簡単に書ける。

プラスとマイナスで重みを変えられる

予測によっては上に外すか下に外すかで影響に差があり、影響が小さくなるように予測したいということも考えられる。

たとえばビールの売れる量を予測するのはビールの仕入れをどうするか考えるためで、売り切れが発生すると機会損失が発生してしまうのでできるだけ避けたく、多少余ってしまっても在庫管理の費用が少し増えるだけで済むとする。それならピッタリの量を予測するよりも少し多めを予測した方がいいと考えられる。

たとえばビールが1足りなかったときの機会損失は10,000円、一方1余ったときの管理費用は1,000円だとする。この場合、次のように定式化してやると都合がいい：

$\displaystyle \left| \begin{array}{rl} \mathrm{min.} & 1000 \sum_i m_i + 10000 \sum_i l_i \\ \mathrm{sub.\ to} & - m_i \le y_i - (a x_i + b) \le l_i \quad (\forall i) \\ & m_i \ge 0, \, l_i \ge 0 \quad (\forall i) \\ \end{array} \right.$

ここでは $m_i$ は余った量、 $l_i$ は足りなかった量を表現してることになる。

これをコードで解いてみる：

# 問題
problem = pulp.LpProblem(sense=pulp.LpMinimize)

# 変数
coef = pulp.LpVariable("coef")
intercept = pulp.LpVariable("intercept")
over = pulp.LpVariable.dicts("over", range(len(air_temp)), lowBound=0)
lack = pulp.LpVariable.dicts("lack", range(len(air_temp)), lowBound=0)

# 目的変数
problem += 1000 * pulp.lpSum(over) + 10000 * pulp.lpSum(lack)

# 制約
for i in range(len(air_temp)):
    predict = coef * air_temp[i] + intercept
    problem += - over[i] <= (beer[i]- predict)
    problem += (beer[i] - predict) <= lack[i]

# 求解
solver = pulp.PULP_CBC_CMD(msg=False)
status = problem.solve(solver)

# 出力
print(pulp.LpStatus[status])  # => Optimal
print(coef.value())  # => 0.86115786
print(intercept.value())  # => 19.705428

さっきまでとはだいぶ違う答えが出てきてる。

図にしてみると以下：

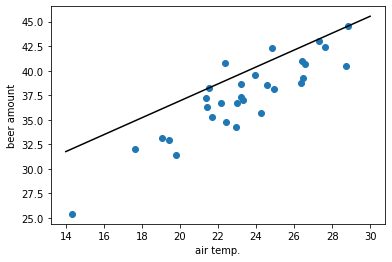
売り切れをできるだけ防ぎつつ在庫もあまり出さないようにする予測になってるのが分かるかと思う。

最大誤差の最小化

ところで誤差をノルムの観点でみると、絶対誤差はL1ノルム、二乗誤差はL2ノルムに相当してるともいえる。ならL∞ノルムに相当する誤差を最小化する線形回帰を考えることもできるんじゃないかというのは自然な発想。これは最大誤差を最小化することになる：

$\displaystyle \min_{a, b} \max_{i} \left|y_i - (a x_i + b)\right|$

これも線形計画問題に簡単に帰着できて、補助変数を一つだけにすればいい：

$\displaystyle \left| \begin{array}{rl} \mathrm{min.} & M \\ \mathrm{sub.\ to} & - M \le y_i - (a x_i + b) \le M \quad (\forall i) \\ & M \ge 0 \\ \end{array} \right.$

コードにするとこんな感じ：

# 問題
problem = pulp.LpProblem(sense=pulp.LpMinimize)

# 変数
coef = pulp.LpVariable("coef")
intercept = pulp.LpVariable("intercept")
max_error = pulp.LpVariable("max_error", lowBound=0)

# 目的変数
problem += max_error

# 制約
for i in range(len(air_temp)):
    predict = coef * air_temp[i] + intercept
    problem += - max_error <= (beer[i]- predict)
    problem += (beer[i] - predict) <= max_error

# 求解
solver = pulp.PULP_CBC_CMD(msg=False)
status = problem.solve(solver)

# 出力
print(pulp.LpStatus[status])  # => Optimal
print(coef.value())  # => 1.0328874
print(intercept.value())  # => 14.12233

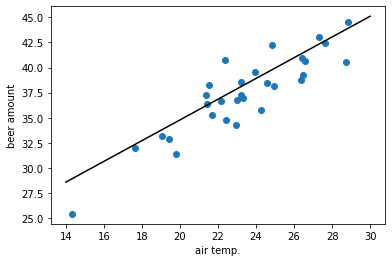
これの使いどころとしては、個々の多少の誤差はどうでもいいので、予測からの誤差の幅をできるだけ小さくしたいというとき。たとえば交通量を予測するとして、誤差がキャパをオーバーすると渋滞になってしまうので、誤差の最大値をできるだけ抑えるような予測をしたいとかがあるかもしれない。普通に流れてるときは予測に誤差があっても問題なくて、逼迫時だけ問題にしたいイメージ。

ということで、当たり前だとスルーしてたことも踏み込んでみるといろいろ面白い。

今日はここまで！