いものやま。

雑多な知識の寄せ集め

ベイズ統計学を学んでみた。（その3）

数学 統計

前回は確率変数を定義した。

今回は分布を定義する。

分布

確率変数は起こりうる事象の集合だった。

となると、それぞれの事象がどれくらい起こりやすいかが問題となる。

そこで、確率変数 Xの要素 x \in Xがどれくらい起こりやすいかを関数 D\langle X\rangle : X \rightarrow \mathbb{R}_{\ge 0}で表すことにし、この関数を分布と呼ぶことにする。

たとえば、サイコロ1個を振るときの出目を確率変数 Xとすると、 X = \{1, 2, 3, 4, 5, 6\}であり、 どの目も同じ出やすさだとすれば、分布 D\langle X \rangleは

D\langle X \rangle (x) = 1\quad(\forall x \in X)

となる。

あるいは、実はイカサマサイコロで1だけ他の目よりも2倍出やすいなら、分布 D\langle X \rangleは

D\langle X \rangle (x) = \begin{cases} 2 & (x = 1) \\ 1 & (x = 2, \ldots, 6) \\ \end{cases}

となる。

記法に関する補足

この D\langle X\rangleという書き方は珍しいけれど、一種のジェネリクスみたいなものだと思ってほしい。 本当は、確率変数 Xの分布が f: X \rightarrow \mathbb{R}_{\ge 0}、確率変数 Yの分布が g: Y \rightarrow \mathbb{R}_{\ge 0}、 ・・・といった感じで、確率変数ごとにそれぞれ関数を用意すべきなんだけど、それだとアルファベットが足りなくなる。 そこで、 D\langle X\rangleと書いたら確率変数 Xの分布だし、 D\langle Y\rangleと書いたら確率変数 Yの分布だとすることで、使うアルファベットを節約している。

ちなみに、そういう場合、普通は添字にして D_Xや D_Yのように書くことが多い。 ただ、確率変数が複数ある場合は添字がとても複雑になってくるので、ツラいことになる。 そこで、添字にする代わりに山括弧で囲うことにした。 e^xを \exp(x)と書くようなものだと捉えれば分かりやすいと思う。

また、同じ確率変数に対して何種類かの分布を考えることもある。 その場合は、1つ目の分布が D_1\langle X\rangle、2つ目の分布が D_2\langle X\rangle、 ・・・といった感じで区別することにする。

連続確率変数に対する分布

分布は連続確率変数に対しても考えることができる。

たとえば、長さ1cmのモノを定規で測ったとすると、定規の質とか測り方で誤差が出たりする。 そこで、観測された長さを確率変数 Yで表すことにすると、誤差が1mm以内だとすればすれば Y = \{y \in \mathbb{R} | 0.9 \le y \le 1.1 \}で、誤差の出やすさが線形だとすれば、分布 D\langle Y\rangleは

D\langle Y\rangle (y) = 1 - 10 |y - 1|\quad(0.9 \le y \le 1.1)

となる。

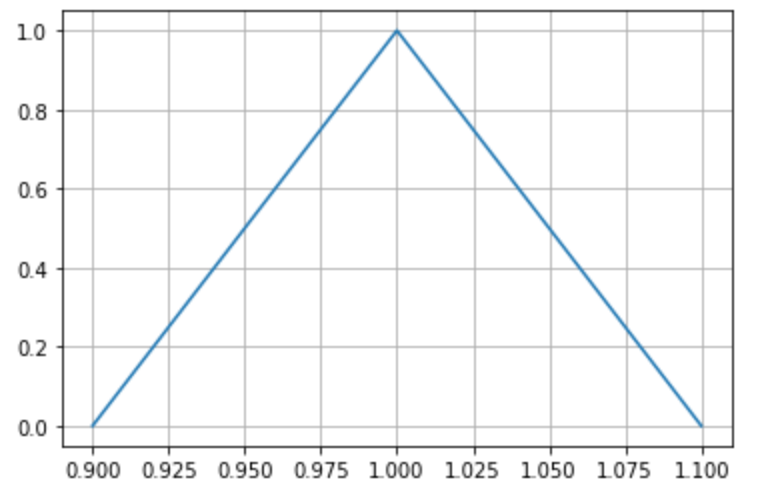
f:id:yamaimo0625:20210327221142p:plain
D\langle Y\rangle (y)のグラフ

比例尺度

一つ重要なのは、分布の値は比例尺度だということ。

比例尺度というのは、2つの値の相対的な比率にだけ意味があって、絶対的な値には意味がないものをいう。

たとえば長さが分かりやすくて、「100cm」や「150cm」といったときに「100」とか「150」という数字には意味がなくて、その比率（2:3）にだけ意味がある。 実際、単位を変えて「1m」と「1.5m」とすると、それぞれの数字は「1」と「1.5」と変わってしまうけど、比率は「1:1.5 = 2:3」と変化がない。 つまり、本質的に比率だけが意味をもっている。

だから、先のサイコロの例で「ん？ なんで D\langle X\rangle(x) = \frac{1}{6}じゃなくて D\langle X \rangle(x) = 1なんだろう？」と思った人もいると思うんだけど、これはどちらの分布も本質的に同じになるから。

実際、 D_1\langle X\rangle(x) = 1、 D_2\langle X\rangle(x) = \frac{1}{6}としたそれぞれについて、分布の2つの値の比率を確認してみると、

D_1\langle X\rangle(x) : D_1\langle X\rangle(y) = 1 : 1\quad(\forall x, y \in X)

で、

D_2\langle X\rangle(x) : D_2\langle X\rangle(y) = \frac{1}{6} : \frac{1}{6} = 1 : 1 \quad(\forall x, y \in X)

なので、 D_1\langle X\rangleも D_2\langle X\rangleも同じ比率になっている。 つまり、どちらも本質的には同じ分布であるといえる。

ちなみに、連続確率変数で確率密度関数を考えたとき、その値は1を越える場合もあるし、その1点で積分しても確率は常に0になってしまうしで、じゃあ確率密度関数の値って何なんだ？と疑問に思った人も多いと思う。 自分もその一人。 それに対する答えがこれ（＝確率密度関数の値は比例尺度である）だと自分は思っている。

さて、分布の値は比例尺度なので、上で見たように、本質的には同じ分布が複数あることになる。 けど、それは厄介なので、その対処を考えていくことになる。

今日はここまで！