紙を三等分に折る方法。

昨日、『数学ガール・乱択アルゴリズム』の感想を書いていて、作図について触れたときに、そういえばと思い出したので。

今日は、作図での掛け算、割り算の方法と、その考え方を応用した、紙を三等分に折る方法を紹介したい。

作図で掛け算

まずは、作図で掛け算を行う方法。

例えば、ある長さを $n$ 倍（ $n$ は自然数）したいとする。
そのときの手順は、以下：

$n$ 倍したい線分ABの端点Aから、半直線ALを伸ばす
半直線ALの端点Aから、コンパスで任意の長さで印をつける（その点をUとする）
続けて、半直線AL上に同じ長さで合計 $n$ 個の印をつける（ $n$ 個目の印のある点をNとする）
線分ABの端点Bから線を伸ばし、半直線ABにする
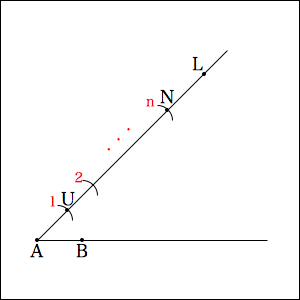
線分BUを引く
点Nを通り、線分BUに平行な線分CN（点Cは半直線ABとの交点）を引く
線分ACが求めたい長さ

なんでこれで線分ABを $n$ 倍出来たかというと、相似を使っていて、線分BUと線分CNが平行になっているので、三角形ABUと三角形ACNは相似な三角形になっていて、AU:ANが1: $n$ なので、AB:ACも1: $n$ になるから。

もっとも、 $n$ 倍するだけなら、このように相似を使わなくてもコンパスでABの長さを $n$ 回分とってやれば（＝ABを $n$ 回足せば）いいんだけど、この相似の考え方を知っていると、次の割り算や、有理数、平方根の掛け算に応用することが出来る。

作図で割り算

さて、次は作図で割り算を行う方法。

ここでは、ある長さを $\frac{1}{n}$ （ $n$ は自然数）にすることを考える。

これは、先ほどの掛け算と同様にするんだけど、AU:ANがAC:ABと等しくなるようにCを作図することで、ACがABの $\frac{1}{n}$ になるようにする。

$\frac{1}{n}$ にしたい線分ABの端点Aから、半直線ALを伸ばす
半直線ALの端点Aから、コンパスで任意の長さで印をつける（その点をUとする）
続けて、半直線AL上に同じ長さで合計 $n$ 個の印をつける（ $n$ 個目の印のある点をNとする）
線分BNを引く
点Uを通り、線分BNに平行な線分CU（点Cは線分ABとの交点）を引く
線分ACが求めたい長さ

このように、相似をうまく使うことで、割り算も出来るようになる。

有理数、平方根の作図

さらに、自然数の掛け算と割り算が出来るようになったので、これを組み合わせることで、有理数の掛け算も可能になる。

そして、三平方の定理を使えば根号も作図できるので、これを相似を使った掛け算の方法と組み合わせることで、平方根の掛け算も可能になる。
すごい！

例えば、線分ABを $\sqrt{3}$ 倍した線分ACを得たかったら、掛け算の手順の中で

半直線AL上に2AU=ADとなるような点Dをコンパスを使って作図
点A、点Dから、コンパスを使ってAE=DE=ADとなるような点Eを作図（つまり、正三角形ADEを作図）
線分EUを引く（この長さが三平方の定理から $\sqrt{3}$ AUとなっている）
コンパスを使って半直線AL上にAN=EUとなるような点Nを作図
（以下略）

とすればいい。

なお、これらの掛け算、割り算は、次の本に書かれていた方法。（のはず。手元にないので確認は出来ない・・・）

定木とコンパスで挑む数学―四則演算から作図不能問題まで (ブルーバックス)

作者: 大野栄一
出版社/メーカー: 講談社
発売日: 1993/10
メディア: 新書
クリック: 1回
この商品を含むブログを見る

紙を三等分に折る方法

さて、タイトルに書いた「紙を三等分に折る方法」。
A4の紙を細長い封筒に入れるときとか、紙を三等分に折りたいときというのは結構ある。（と思う）
けど、ちゃんと三等分するとなると、なかなか難しい・・・

そんなときに、これまでに書いた相似を使った方法を応用して、紙を三等分に折る方法を昔考えた。

具体的には、以下のようにする：

紙を半分に折る
紙全体の対角線となる線を折る
紙の半分のサイズの長方形の対角線となる線を折る
2.と3.の対角線の交わる点を通るように紙を折る
残りを半分に折る

これで三等分に！

なお、こんなにガンガン折ってしまってはダメな場合、端っこにちょこっとずつ折り目をつけていくと、紙全体にはそれほど折り跡が残らずに三等分に折ることが出来る。

ここでは三角形の相似を2つ使っている。

まず、三角形PAMと三角形PCBが相似な三角形になっていて、その比は、AM:CB=1:2であることから、1:2。
これによって、PA:PCが1:2に分割されている。

次に、三角形APHと三角形ACDが相似になっていて、その比は、PA:PCが1:2であることから、AP:ACは1:3。
なので、AH:ADも1:3で、つまり、AHの長さはAD全体の $\frac13$ になっているので、三等分できている、と。

つまり、1という長さ（AM）と2という長さ（BC）を作ることは出来るので、それを一本の直線（AC）上に比として落とし込んで（AP:PC=1:2）、そうすれば、(端から分割している点までの距離):(端から端までの距離)は1:3になる（AP:AC=1:3）ので、作図による割り算と同じ原理から（線分CDと線分PHは平行）、線分ADを $\frac13$ にした線分AHが得られる、というわけ。

ちなみに、「紙を折る」という操作の加わった作図の場合、「定木とコンパス」による作図よりも強力になっていて、定木とコンパスでは不可能な角の三等分とかも出来るようになるみたい。（詳しくは調べてないけど）
折紙の数学 - Wikipediaとかが参考になるかも。

折り紙については、次の本も面白かった。
実際に折るのはすごく難しいけどw