ツイッターを見ていたら、次のような興味深いツイートが。
0のノードから始めて数字の先頭の数だけ黒い矢印に進み、白い矢印を一つだけ進み、次の数だけ黒い矢印を進み……とたどるとその数字を7で割った余りが分かるグラフ https://t.co/1hk7toN33y
— ABA (@abagames) November 9, 2015
ちょっと分かりにくいけど、例えば325を7で割った余りが知りたかったら、リンク先のグラフで
- 0からスタート
- 100の位は「3」なので、黒い矢印に従って3つ進む(3に行く)
- 白矢印に従って進む(2に行く)
- 10の位は「2」なので、黒い矢印に従って2つ進む(4に行く)
- 白い矢印に従って進む(5に行く)
- 1の位は5なので、黒い矢印に従って5つ進む(3に行く)
よって、325を7で割った余りは3、と。
実際、325 / 7 = 46 あまり 3なので、合ってる。
原理
どうしてこうなるのか考えてみたんだけど、試しに少し書き出してみると、原理が見えてくる。
以下では余りを求める計算を%で表すとして、小さい数から順番に試してみると、
- 10の位が0の場合
- 0 % 7 = 0
- 1 % 7 = 1
- 2 % 7 = 2
- 3 % 7 = 3
- 4 % 7 = 4
- 5 % 7 = 5
- 6 % 7 = 6
- 7 % 7 = 0
- 8 % 7 = 1
- 9 % 7 = 2
- 10の位が1の場合
- 10 % 7 = 3
- 11 % 7 = 4
- 12 % 7 = 5
- 13 % 7 = 6
- 14 % 7 = 0
- 15 % 7 = 1
- 16 % 7 = 2
- 17 % 7 = 3
- 18 % 7 = 4
- 19 % 7 = 5
- 10の位が2の場合
- 20 % 7 = 6
- 21 % 7 = 0
- 22 % 7 = 1
- 23 % 7 = 2
- (省略)
- 10の位が3の場合
- 30 % 7 = 2
- (省略)
- 10の位が4の場合
- 40 % 7 = 5
- (省略)
- 10の位が5の場合
- 50 % 7 = 1
- (省略)
- 10の位が6の場合
- 60 % 7 = 4
- (省略)
つまり、nを1の位の数字としたときに、
- (0 + n) % 7 ≡ 0 + n (mod 7)
- (10 + n) % 7 ≡ 3 + n (mod 7)
- (20 + n) % 7 ≡ 6 + n (mod 7)
- (30 + n) % 7 ≡ 2 + n (mod 7)
- (40 + n) % 7 ≡ 5 + n (mod 7)
- (50 + n) % 7 ≡ 1 + n (mod 7)
- (60 + n) % 7 ≡ 4 + n (mod 7)
- (70 + n) % 7 ≡ (0 + n) % 7 ≡ 0 + n (mod 7)
- (省略)
となっているので、10の位の数字に応じて、その数字の余りのスタート地点となる位置に移動し(これが白矢印による移動)、1の位の数字の分だけ数を増やせば(これが黒矢印による移動)、2桁の数字を7で割った余りが求まることになる。
これで2桁の数字を7で割った余りが求まることが分かったら、次は、筆算と同様に考えていけばいい。
例えば、325を7で割る筆算を考えた場合、最初、最上位の2桁の32を7で割り、次はその余りを10の位、5を1の位とする2桁の数を7で割るわけだから、
- 最初は最上位の2桁数字、32の10の位の数字3を見て、白矢印に従って2に進む
- 最上位の2桁数字、32の1の位の数字2を見て、黒矢印に従って2つ進むことで、4に進む(=32 / 7 の余りは4)
- 次の最上位の2桁の数字は、この余りの4と1の位の5を組合せた45
- 次の最上位の2桁の数字、45の10の位の数字4を見て、白矢印に従って5に進む
- 次の最上位の2桁の数字、45の1の位の数字5を見て、黒矢印に従って5つ進むことで、3に進む(=45 / 7 の余りは3)
つまり、筆算で、最上位の2桁から計算を始め、余りの数字に次の位の数字を下ろしてきて新たな2桁の数字にして、計算を繰り返していく、というのが、白矢印による移動(直前の計算で求めた余りを、次の2桁の数字の10の位の数字と見なしている)と黒矢印による移動(下ろしてきた次の位の数字を1の位の数字と見なしている)の繰り返しとして、表現されている、というわけ。
(伝わるかな・・・?)
1桁の各数字で割った余りを求めるグラフ
原理が分かってしまえば、他の1桁の数字で割った余りを求めるグラフというのも、簡単に分かる。
具体的には、まず0からn-1までの数字を用意して、それぞれを黒矢印で繋ぐ。 そのあと、0, 10, 20, 30, ・・・を割った余りを求め、その10の位の数字と余りの数字を白矢印で繋いでやればいい。
2で割った余りを求めるグラフ
最初は2。
0%2=0, 10%2=0なので、次のようになる。

これは、白矢印で常に0に戻ってくるので、つまり、1の位の数字だけ見れば、偶数か奇数かがすぐに分かる、ということを意味している。
3で割った余りを求めるグラフ
次は3。
0%3=0, 10%3=1, 20%3=2なので、次のようなグラフになる。
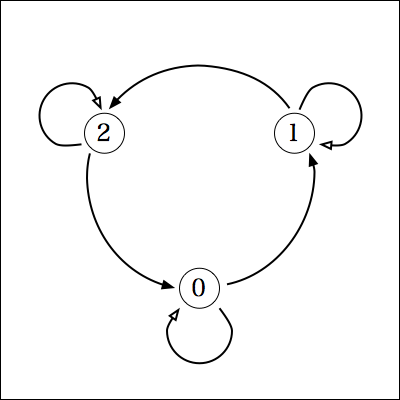
ここで興味深いのは、白矢印は全部自分自身に戻ってきているということ。
これがどういう意味かというと、つまり、各位の数字の合計分だけ黒矢印の方向に進むのと同じ結果になってるということで、これは、3で割った余りが、各位の数字を全部足して3で割った余りと等しい、という事実と一致している。
4で割った余りを求めるグラフ
続いて4。
0%4=0, 10%4=2, 20%4=0, 30%4=2なので、次のようなグラフになる。
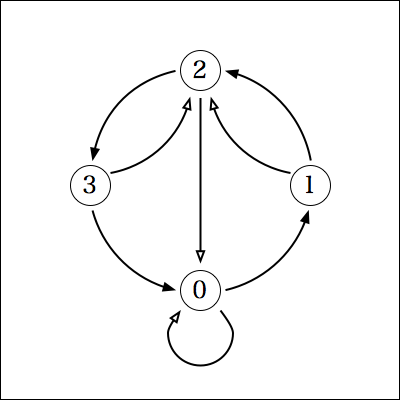
このグラフの特徴は、どの位置からも白矢印に従って2回移動すると、0の位置に必ず戻る、ということ。
これの意味するところは、100も200も300も4で割り切れるということで、すなわち、4で割った余りは、下2桁の数字を4で割った余りと一致する、ということが分かる。
(ただ、グラフ上での移動だけ見た場合、白矢印での移動の間に黒矢印による移動が挟まるので、その移動の仕方から上記の事実を引き出すというのは出来なそう・・・)
5で割った余りを求めるグラフ
次は5。
0, 10, ... , 40を5で割った余りはどれも0なので、次のようなグラフになる。
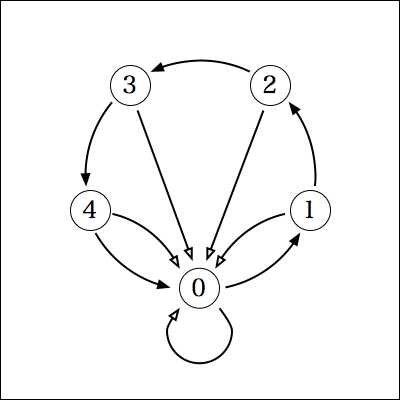
これも2で割った余りを求めるグラフと同じで、白矢印は常に0に戻ってくるので、1の位の数字だけ見れば、5で割った余りが分かるということが分かる。
6で割った余りを求めるグラフ
次は6。
0%6=0, 10%6=4, 20%6=2, 30%6=0, 40%6=4, 50%6=2なので、次のようなグラフになる。
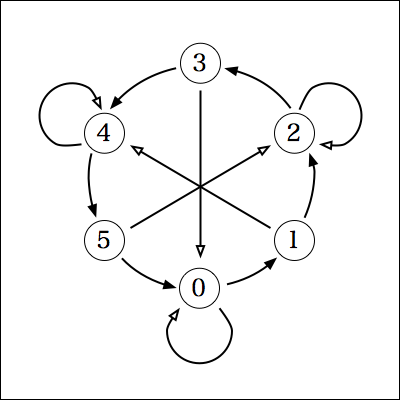
グラフの形から何か言えそうな気もするんだけど、うーん・・・
7で割った余りを求めるグラフ
7については、最初に行った計算から、次のグラフになる。
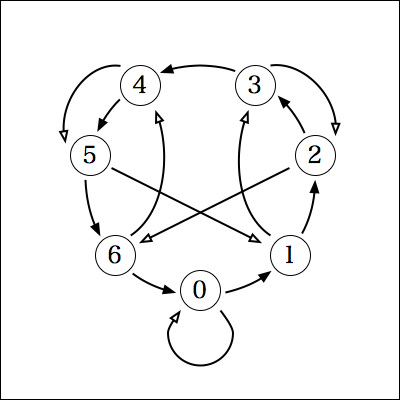
これは最初のリンク先のグラフと同じ。
8で割った余りを求めるグラフ
続いて8。
0%8=0, 10%8=2, 20%8=4, 30%8=6, 40%8=0, 50%8=2, 60%8=4, 70%8=6なので、次のようなグラフになる。
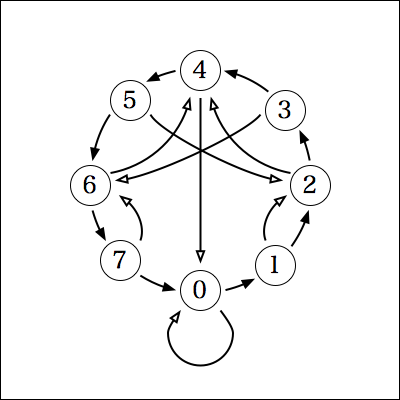
これも4のときと同様に、どの位置からも白矢印に従って3回移動すると、0の位置に必ず戻るようになっている。
なので、1000, 2000, 3000, ....が8で割り切れることを意味していて、下3桁の数字を8で割った余りが、8で割ったときの余りと一致することを導ける。
9で割った余りを求めるグラフ
最後に9。
0%9=0, 10%9=1, 20%9=2, 30%9=3, 40%9=4, 50%9=5, 60%9=6, 70%9=7, 80%9=8なので、次のようなグラフになる。
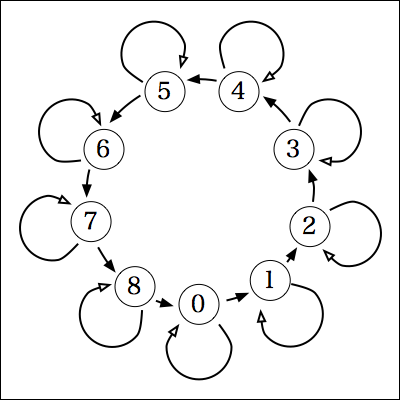
これも3のときと同じで、白矢印は全部自分自身に戻ってきている。
なので、3のときと同様に考えることが出来て、すなわち、9で割った余りは、各位の数字を全部足した数を9で割れば求まる、ということが分かる。
2桁以上の数字で割った余りが求まるグラフは・・・?
1桁の数字で割った余りが求まるグラフが得られたので、次は2桁以上の数字で割った余りが求まるグラフが得られるのかが気になるところ。
実のところ、2桁以上になっても同じ方法で求めることが出来るみたい。
例えば、12で割った余りを求めるグラフだと、次のようになる。
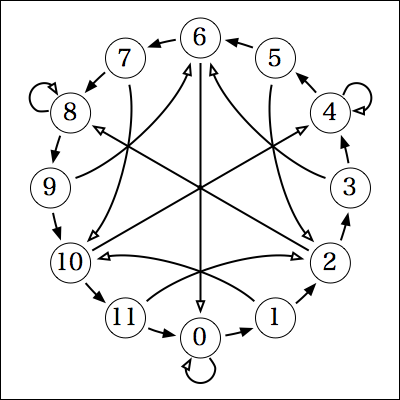
なんかキレイw
で、これで実際に、例えば2513 / 12の余りを出してみると、
- 0から黒矢印に従って2進む(2に行く)
- 白矢印に従って8に行く
- 黒矢印に従って5進む(1に行く)
- 白矢印に従って10に行く
- 黒矢印に従って1進む(11に行く)
- 白矢印に従って2に行く
- 黒矢印に従って3進む(5に行く)
となるので、グラフは余りが5だと主張しているわけだけど、実際、2513 / 12 = 209 あまり 5なので、合ってる。
グラフの生成方法について、より一般的な話にすると、余りの数列を10ごとに区切り、その区切りの一番先頭の数字を拾っていると考えることが出来るので、10を「割る数」で割ったときの余りを差分として生成された等差数列を、各位置からの白矢印の行き先とすればいい。(※「割る数」を法として計算する)
何を言ってるか分からないかもしれないので、具体的な例で示すと、
- 2で割った余りを求めるグラフ
- 10%2=0なので、生成される等差数列は0, 0で、0, 1からの白矢印の行き先は両方とも0
- 3で割った余りを求めるグラフ
- 10%3=1なので、生成される等差数列は0, 1, 2で、0, 1, 2からの白矢印の行き先は自分自身
- 4で割った余りを求めるグラフ
- 10%4=2なので、生成される等差数列は0, 2, 0(≡4), 2(≡6)で、0, 1, 2, 3からの白矢印の行き先は、それぞれ0, 2, 0, 2
- 5で割った余りを求めるグラフ
- 10%5=0なので、生成される等差数列は0, 0, 0, 0, 0で、0, 1, 2, 3, 4からの白矢印の行き先はすべて0
- 6で割った余りを求めるグラフ
- 10%6=4なので、生成される等差数列は0, 4, 2(≡8), 0(≡12), 4(≡16), 2(≡20)で、0, 1, 2, 3, 4, 5からの白矢印の行き先は、それぞれ0, 4, 2, 0, 4, 2
- これは、10≡-2 (mod 6)とみて、生成される等差数列を0, 4(≡-2), 2(≡-4), 0(≡-6), 4(≡-8), 2(≡-10)と、逆回りで考えることも出来る
- (省略)
- 12で割った余りを求めるグラフ
- 10≡-2 (mod 12)なので、生成される等差数列は0, 10, 8, 6, 4, 2, 0, 10, 8, 6, 4, 2で、0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11からの白矢印の行き先は、それぞれ0, 10, 8, 6, 4, 2, 0, 10, 8, 6, 4, 2
という感じ。
この方法を使えば、簡単にグラフを生成することが出来る。
(もっとも、割る数が大きくなると、描くのが大変になるけど)
今日はここまで!