久々に。
前回までは、非連想的な問題である、n本腕バンディット問題を扱っていた。
今回からは、元々考えていた、強化学習について学んでみた。(その3) - いものやま。で述べたような状況ーーすなわち、行動の選択によって、状態がどんどん変化していってしまうような状況ーーを考えていく。
状態遷移のモデル
ところで、行動の選択によって状態がどんどん変化していってしまう場合、何が難しいのかというと、それはそれぞれの行動がどれくらい後にもらえる報酬に寄与したのかがパッとは分からないということだ。
例えば、最初の猿の例であれば、大きい箱を選ぶという行動と小さい箱を選ぶという行動はそれ自体では報酬がもらえず、後にもらえる報酬もそのあとに選ぶ行動によって変わってきてしまう。
なので、それぞれの行動の価値をどう考えればいいのかが難しい。
これを論理的に考えていくことが出来るようにするために、状態遷移のモデルというものを考えていく。
まず、報酬とは別に、収益というものを考える。
これは、報酬が行動
を選択した直後にもらえるものであるのに対し、行動
を選択したことで、最終的に合計でどれくらいの報酬を得られたのかを示すものとなっている。
すなわち、
と定義される。
なお、は割引率と呼ばれるもので、将来もらえる報酬をどれくらい現在の価値として考慮に入れるかを表すパラメータになる。
例えば、なら、直後の報酬のみを考えることになるし、
なら、将来もらえる報酬をすべてそのまま現在の価値として考慮に入れることになる。
このように収益を定義すると、それは、その状態や行動の最終的な価値を意味するものとなってくる。
ただ、収益を上のように定義したけれど、当然、収益は行動
のあとの状態
や報酬
、さらに、その状態で選択される行動
によって変わってくることになる。
なので、実際には収益の期待値というものを考えていかないといけない。
そして、最終的にはこの収益の期待値が最大になるようにすることを考えることになる。
収益の期待値を考えることが出来るようにするために、状態遷移の確率、報酬の期待値
を、次のように定義する。
すなわち、それぞれ、状態のときに行動
を選択して状態が
になる確率と、そのときに得られる報酬の期待値を表す。
図に表すと、次のような感じ。
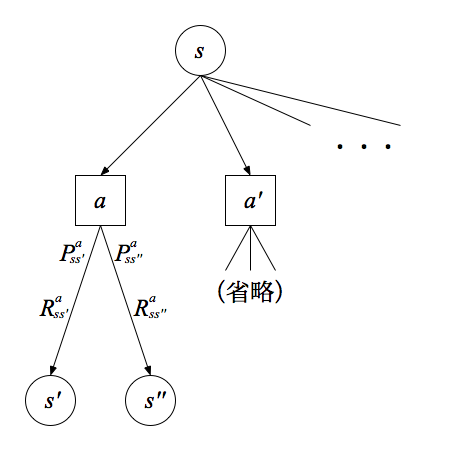
これらの確率、期待値は、エージェントがその値を知ることが出来るかは別として、環境によって決まってくる。
すなわち、これらの値が状態遷移のモデルを表現することになる。
とくに、各状態と行動の繋がり、および、状態遷移の確率と報酬の期待値を表したグラフを、状態遷移グラフと呼んだりする。
状態価値ベクトル、行動価値ベクトル
ただし、これだけだとまだ収益の期待値は計算できない。
というのも、収益の期待値は、エージェントがどのように行動を選択するのかという確率ーーすなわち、方策(ポリシー)ーーに影響を受けるからだ。
逆に言えば、状態遷移のモデルがあるときに、ある方策]が与えられれば、それに対応した収益の期待値というのは計算可能になってくる。
そこで、ある方策が与えられたとして、状態の価値を表すベクトル
(これを状態価値ベクトルと呼ぶことにする)、および行動の価値を表すベクトル
(これを行動価値ベクトルと呼ぶことにする)を、収益の期待値を使って次のように定義する。
なお、本ではこれらをそれぞれ状態価値関数、行動価値関数
としているけれど、これらは方程式内で変数になるので、ベクトルと解釈しておいた方が分かりやすいと思う。
(関数が方程式の変数になっているという考え方がすんなり受け入れられるのであれば、本の記述でも問題ないのだけど)
ところで、この定義について計算をしていくと、
となることから、状態価値ベクトルの各要素
の間には、次の関係が成り立つ。
したがって、これはに関する連立一次方程式になっていて、Bellman方程式と呼ばれている。
なお、行動価値ベクトルについても同様の展開が出来て、次のような連立一次方程式が得られる。
(これもBellman方程式と呼ばれる)
Bellman方程式があることから、これを解くことが出来れば、ある方策でのそれぞれの状態、行動の価値を計算できることが分かる。
さらに、方策を変更することで状態、行動の価値を向上させることが出来れば、それぞれの状態でより価値の高い行動を選択できるようになっていることになる。
そこで、問題となってくるのは、次の3つ。
- 方策が与えられたときに、Bellman方程式をどうやって解けばいいのか。(方策評価)
- Bellman方程式の解を改善する(=収益の期待値を大きくする)ような方策をどうやって得ればいいのか。(方策改善)
- そもそも、状態遷移のモデル(状態遷移の確率、および、報酬の期待値)が分からない場合、どうすればいいのか。
明日以降は、これらを順番に片付けていくことになる。
今日はここまで!

- 作者: Richard S.Sutton,Andrew G.Barto,三上貞芳,皆川雅章
- 出版社/メーカー: 森北出版
- 発売日: 2000/12/01
- メディア: 単行本(ソフトカバー)
- 購入: 5人 クリック: 76回
- この商品を含むブログ (29件) を見る